WhatsApp:
+353 87 202 0389
My Advice For Leaving Cert Maths
The Leaving Certificate is the final exam for secondary school students in Ireland. There are 36 subjects available, and the only mandatory subjects for the Leaving Cert are English, Irish, and Mathematics. Including these three, a student MUST sit a minimum of 6 subjects.
All Leaving Cert subjects can be studied at either Higher Level (HL) or Ordinary Level (OL) except for Irish and Mathematics, which can be studied at the Foundation Level (FL) as well. Among all the Leaving Cert subjects, Mathematics is the most required subject for enrollment at almost all Irish universities.
That is why this article will provide you with a complete overview of the Leaving Cert Maths with the latest adjustments for 2022. It’ll include:
- What Is Leaving Cert Maths?
- LC Maths Syllabus
- Assessment Method
- LC maths HL
- LC Maths OL
- LC Maths FL
- Grading System
- Exam Layout
- Highest Possible Grade
- Bonus Tips to Ace LC Maths
The Leaving Cert Timetable 2024 has been published! And we’ve prepared a 2-hour maths crash course which is the final boost your child needs to be prepped, ready, and confident as they walk into their exams.
What Is Leaving Cert Maths?
Leaving Cert Mathematics is a secondary level subject that builds on the students’ knowledge from the Junior Cycle and develops mathematical skills needed for continuing further higher education and career.
Leaving Cert Maths is designed as a 2-years course and can be studied at three levels- Higher Level (HL), Ordinary Level (OL), and Foundation level (FL). Each level follows a separate syllabus that matches each level’s difficulty.
There are two examination papers at the HL and the OL (Paper 1 and Paper2). Both papers are given 2.5 hours (150 minutes) to complete.
There is only one examination paper for the FL and it is also given 2.5 hours (150 minutes) to complete.
LC Maths Syllabus
The current syllabus for Leaving Cert Mathematics for all levels was introduced in 2015. It consists of 5 strands:
- Statistics and Probability
- Geometry and Trigonometry
- Number
- Algebra
- Functions

In each strand, the learning outcomes are set out in terms of the complexity of the Foundation level, the Ordinary level, and the Higher level.
For a detailed but simplified overview, read my article on Leaving Cert Maths Syllabus.
Assessment Methods
At Leaving Cert Maths Ordinary Level and Higher Level, there are two assessment components. As in both levels have 2 written exams papers. They are:
- Paper 1
- Paper 2


Each paper will contain two sections – Section A and Section B.
- Section A will address core mathematics topics, focusing on concepts and skills.
- Section B will include questions that are context-based applications of mathematics.

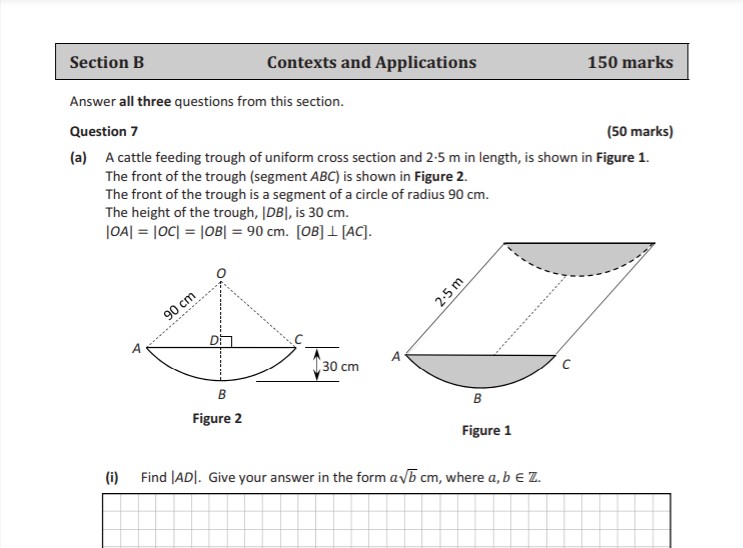
At the Foundation Level LC Maths, there is only one assessment component, i.e one written paper. It will also follow the above-mentioned 2 section layout of the HL and the OL.

Leaving Cert Maths Higher Level (HL)
Leaving Cert Mathematics at the Higher level is geared to the learners who mainly wish to proceed with their higher education in universities in mathematics-focused courses.
Course Contents
Some elements of the courses may come up in either paper.
Paper 1
- Algebra
- Complex Numbers
- Differentiation
- Financial Maths/ Arithmetic
- Functions
- Indices and Logs
- Integrations
- Number
- Proof by Induction
- Sequences and Series
Paper 2
- Probability
- Statistics and Data
- Coordinate Geometry (Including Constructions and Theorems)
- The Line
- The Circle
- Trigonometry
- Transformations and Enlargements
- Length, Area and Volume
Question Pattern
For Leaving Cert HL Maths, there is no set model for what questions and what topics may appear. Often questions will test you on a few different topics from across the course. That is why it’s better to regularly practice past exam papers as much as you can.
I’ve provided a sample question pattern for you from previous years’ questions:
Paper 1
Section A: Concepts & Skills
| 2021 | 2020 | 2019 | |
|---|---|---|---|
| Q1 | 1. Division of complex numbers 2. Square roots of complex numbers 3. De Moivre’s theorem | 1. Functions – long division 2. Roots of a function/finding missing terms of a function 3. Functions with imaginary roots 4. Modulus | 1. Algebra – undetermined coefficients 2. Algebraic fractions |
| Q2 | 1. Modulus 2. Roots of cubic functions | 1. Complex numbers – simultaneous equations 2. Complex numbers/sequences and series – finding a common ratio of a geometric sequence (dividing complex numbers) 3. De Moivre’s Theorem | 1. Algebra – Plotting a linear graph given the equation/ substitution 2. Proof by induction |
| Q3 | 1. Volume 2. Multiplication of surds 3. Roots of quadratic functions 4. Logs and indices | 1. Composite functions 2. Logs | 1. Factorising by grouping 2. Substitution 3. Differentiation |
| Q4 | 1. Proof by induction 2. Arithmetic sequences | 1. Differentiation – the first derivative 2. Functions – where a line intersects a curve 3. Differentiation – finding the point of inflection | 1. Integration 2. Finding the equation of a function from a graph/ integration/ solving a cubic function |
| Q5 | 1. Differentiation 2. Co-ordinate geometry of the line | 1. Financial maths – amortisation formula to find the monthly payment 2. Financial maths – present value and total mortgage owed | 1. Complex numbers – cubic equations 2. Writing complex numbers in polar forms/ De Moivre’s Theorem |
| Q6 | 1. Quadratic functions 2. Differentiation | 1. Differentiation from first principles 2. Differentiation of an equation containing the natural log 3. Integration | 1. Algebra – irrational equations/ surds/ Statistics – mean, median 2. Proof by contradiction |
Section B: Contexts & Applications
| 2021 | 2020 | 2019 | |
|---|---|---|---|
| Q7 | 1. Sequences and series 2. Trigonometry | 1. Sequences and series – completing the sequence 2. Substituting into the formula for a sequence 3. Algebraic fractions 4. Simplifying algebraic expressions 5. Algebra – solving for n 6. Substitution into a formula 7. Proof by induction | 1. Sequences and series – geometric progressions/ finite series 2. Geometric progressions/ limits of a series |
| Q8 | 1. Cubic functions 2. Differentiation 3. Integration | 1. Trigonometry – trigonometric identities 2. Area 3. Differentiation to find the maximum area 4. Differentiation – rates of change | 1. Trigonometric functions 2. Trigonometric functions 3. Differentiation of trigonometric functions 4. Differentiation – show a function is increasing 5. Differentiation – minimum point, point of inflection |
| Q9 | 1. Indices and logs 2. Differentiation | 1. Substitution into a formula involving indices 2. Logs 3. Integration – average value 4. Differentiation 5. Differentiation/inequality 6. Algebra/ logs | 1. Perimeter/ The Circle/ Algebra 2. Algebra/ Graphing a linear function/ Finding the slope of the graph/ Interpreting the slope 3. Algebra/ Functions/ Area/ Differentiation of a function/ Maximum point of a function |
| Q10 | 1. Functions 2. Differentiation 3. Trigonometry 4. Volume | – | – |
Paper 2
Section A – Concepts & Skills
| 2021 | 2020 | 2019 | |
|---|---|---|---|
| Q1 | 1. Probability | 1. Equation of a line given two points on the line 2. Perpendicular distance from a point to a line 3. Finding the slope of a line given the angle it makes with the x-axis 4. Angle between two lines | 1. Probability – combinations/selections 1. Probability – combinations/selections |
| Q2 | 1. Co-ordinate geometry of the line – point on the line given the equation of the line 2. Perpendicular distance of a point from a line 3. Distance between two points 4. Similar triangles | 1. Finding the center and radius of a circle 2. Distance between two points 3. Trigonometry 4. Circles with centers on the axes 5. Finding the equation of a circle given the radius and a point on the circle | 1. The Line – equation of a line 2. The Line – Finding the equation of a line given the slope and a co-ordinate/ intersection of two lines |
| Q3 | 1. Finding the radius of a circle 2. Circles that touch externally | 1. Trigonometry 2. Sine rule 3. Area of a circle 4. Ratios | 1. The Circle – finding a point on the circle given the equation of circle 2. The Circle – circle with the axes as tangents/ finding the equation of a circle |
| Q4 | 1. Trigonometric proofs 2. Trigonometric equations | 1. Trigonometry – solving trigonometric equations 2. Area of a sector 3. Area of a triangle | 1. Trigonometric proof: cos2Θ = 1 – 2sin2Θ 2. Trigonometry/ angle between two lines |
| Q5 | 1. Volume of a cone 2. Volume of a sphere 3. Distance, velocity, time | 1. Conditional probability 2. Independent events 3. Probability of an outcome in a game | 1. Construction – orthocentre of a triangle 2. Trigonometry/ The Circle/ The Line/ Properties of triangles/ circles/ tangents |
| Q6 | 1. Proof – if two triangles are similar, the lengths of their sides are proportional in order 2. Co-ordinate geometry of the line – axioms and corollaries | 1. Probability 2. Bernoulli trials | 1. Probability – independent events 2. Probability |
Section B – Contexts & Applications
| 2021 | 2020 | 2019 | |
|---|---|---|---|
| Q7 | 1. Trigonometry 2. Distance, velocity, time 3. Area of a triangle 4. Perpendicular distance from a point to a line | 1. Pythagoras’ Theorem 2. Surface area of a cone 3. Sectors 4. Volume of a cone 5. Flow rate – cross-sectional area multiplied by rate | 1. Pythagoras’ Theorem/ Trigonometry/ Area/ Volume 2. Area/ Volume/ 3D shapes |
| Q8 | 1. Normal distribution 2. Z-scores 3. P-tests 4. Probability – Bernoulli trials | 1. Statistics 2. Z-scores 3. 95% confidence interval 4. Sample proportion 5. Hypothesis testing 6. Measures of spread and central tendency | 1. Statistics – hypothesis testing/ interpreting normal distributions/ z-scores 2. Statistics – Interpreting p-values/ sample mean |
| Q9 | 1. Trigonometry 2. Distance, velocity, time 3. Trigonometric functions | 1. Trigonometry 2. Functions 3. Pythagoras’ Theorem 4. Differentiation – minimum value | 1. Trigonometry – cosine rule 2. Sine rule 3. Area of a triangle 4. Area/ radius of a circle 5. Trigonometry – angle of elevation |
| Q10 | 1. Probability 2. Bernoulli trials 3. Z-scores 4. Expected value | – | – |
Leaving Cert Maths Ordinary Level (OL)
Leaving Cert Maths at Ordinary Level is geared to the learners who are beginning to deal with abstract Maths. It must start by offering mathematics that is meaningful and accessible to learners at their present stage of development.
Course Contents
Paper 1
- Algebra
- Complex Numbers
- Differentiation
- Financial Maths/ Airthmatics
- Graphing and Functions
- Number
Paper 2
- Probability
- Statistics
- Co-Ordinate Geometry (Including Constructions and Theorems)
- Trigonometry
- Transformations and Enlargements
Question Pattern
Similar to Leaving Cert Maths HL, there is no set pattern for the Ordinary Level Maths. Practicing the course materials and solving the past exam papers will be the most beneficial for you. You can find all the previous years’ questions here and practice them regularly.
Leaving Cert Maths Foundation Level (FL)
Mathematics at the Foundation level is for those who face difficulties at the Ordinary level. At this level, learners are not required to deal with abstract mathematics. Thus, their experience of mathematics at Leaving Certificate should be approached easily.
It should be noted that the Foundation Level Maths does not carry any CAO Points and fail to fulfill the requirements for university courses that have mathematics prerequisites.
Course Contents
- Number systems
- Arithmetic
- Length, area, volume
- Data, and statistics
- Probability
- Algebra
- Functions
- Coordinate geometry
- Geometry
- Trigonometry
Question Pattern
Similar to Leaving Cert Maths HL and OL, there is no set pattern for the Foundation Level Maths. Practicing the course materials and solving the past exam papers will be the most beneficial for you. You can find all the previous years’ questions here and practice them regularly.
Grading Points System
In 2017, a revised grading system for the Leaving Cert and a new 8-points standard scale was introduced, replacing the previous 14-point grading scale. The points are calculated based on the results of the six best subjects in one year’s LC sitting.
On this new scale, the highest grade is Grade H1 or O1, and the lowest is Grade H8 or O8 at the Higher and Ordinary levels respectively.
| Points at Higher Level | Grades at Higher Level | Percentage (%) | Points at Ordinary Level | Grades at Ordinary Level |
|---|---|---|---|---|
| 100 | H1 | 90-100 | 56 | O1 |
| 88 | H2 | 80-89 | 46 | O2 |
| 77 | H3 | 70-79 | 37 | O3 |
| 66 | H4 | 60-69 | 28 | O4 |
| 56 | H5 | 50-59 | 20 | O5 |
| 46 | H6 | 40-49 | 12 | O6 |
| 37 | H7 | 30-39 | 0 | O7 |
| 0 | H8 | 0-29 | 0 | O8 |
So for example, a student who scores between 90%-100% at the Higher Level Maths, will score an H1 and get 100 points.
A student who scores between 90%-100% at the Ordinary Level Maths will receive an O1 and get 56 points.
Bonus Points For Higher Level Maths
Higher Maths is considered the most time-consuming of all LC subjects, so it was decided to introduce a bonus point system. For Grades H1 – H6 in Higher Level Mathematics, 25 bonus points will be added.
For example, if an applicant receives an H5 grade in LC Maths, an additional 25 points will be added to the 56 points for his H5 grade. His Higher Level Mathematics now carries a points score of 81.
However, for this to apply, Maths must be one of your top six points, and you must pass it.
Exam Layout
The exam layouts for the Leaving Cert Maths HL, OL, and FL are given below.
This is to be noted that, this exam layout for LC Maths was applicable until 2019. Due to the pandemic, a new exam layout has been followed from 2020 and the 2022 adjustments for LC Maths are given in the next section.
Higher Level
Both Paper 1 and Paper 2 of the Leaving Cert Maths HL are 2.5 hours long and have 2 sections.
- Section A – Concepts & Skills (150 Marks)
- No choice
- 6 questions x 25 marks

- Section B – Contexts & Applications (150 Marks)
- No choice
- 2 or 3 or 4 questions
- Marks per question may vary

You must answer all 9 questions of both the papers.
Ordinary Level
Both Paper 1 and Paper 2 of the Leaving Cert Maths OL are 2.5 hours long and have 2 sections.
- Section A – Concepts & Skills (150 Marks)
- No choice
- 6 questions x 25 marks
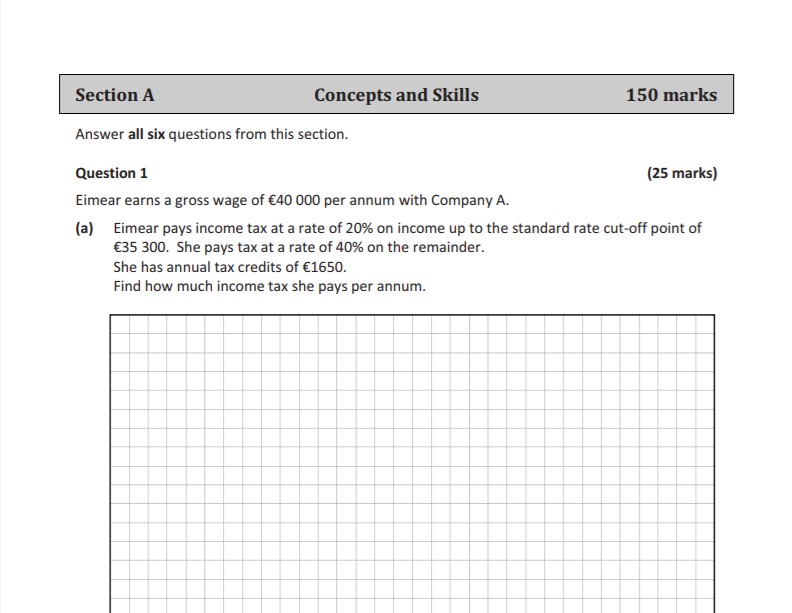
- Section B – Contexts & Applications (150 Marks)
- No choice
- 2 or 3 or 4 questions
- Marks per question may vary
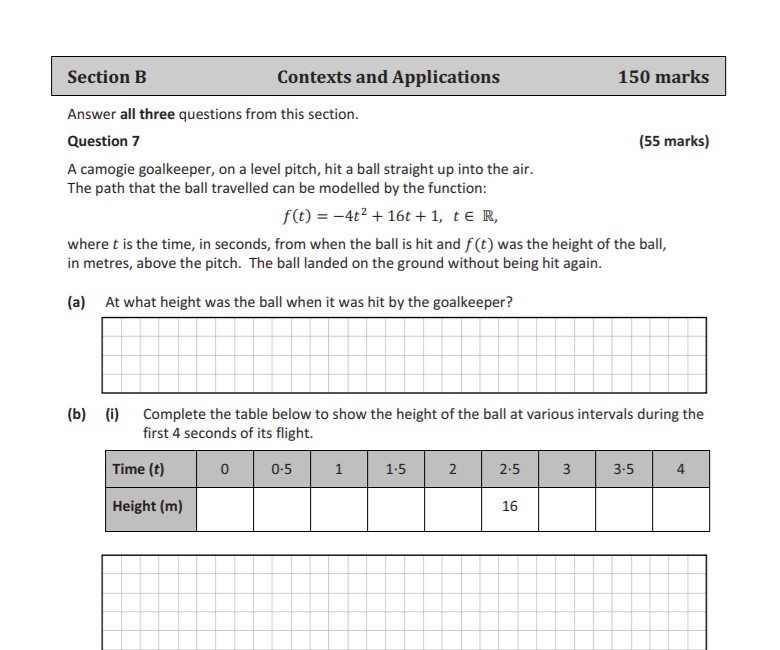
You must answer all 9 questions of both the papers.
Foundation Level
The exam is 2.5 hours long and has 2 sections.
- Section A – Concepts & Skills (200 Marks)
- No choice
- 8 questions x 25 marks
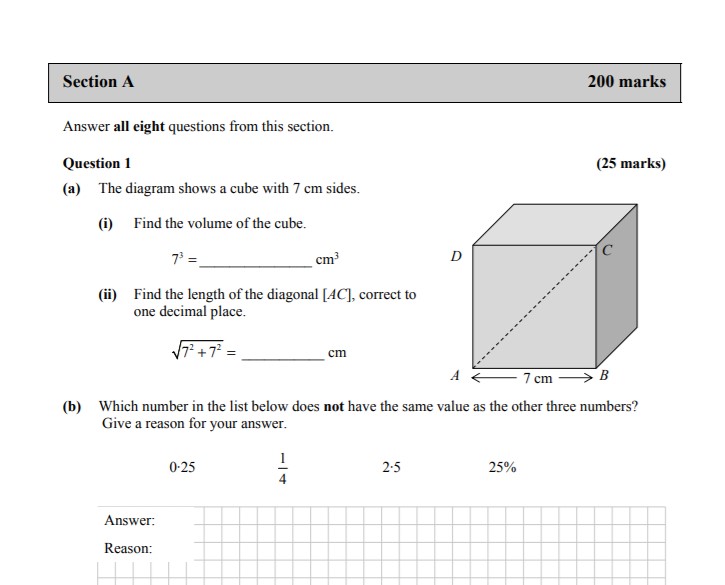
- Section B – Contexts & Applications (100 Marks)
- No choice
- 2 or 3 or 4 questions
- Marks per question may vary

You must answer all questions from both sections.
2022 Adjustments For Leaving Cert Maths
Higher Level And Ordinary Level
Section A: Concepts & Skills (150 Marks)
- Candidates will have a choice of 5 questions from 6, instead of having no choice.
- Each question will be worth 30 marks, as opposed to 25.
- However, Section A will still be worth the same in total as previous years (5X30=150 marks).
Section B: Contexts & Applications (150 Marks)
- Candidates will choose 3 questions from 4 instead of having no choice.
- Each question will be worth 50 marks.
- Section B will be worth the same in total as previous years (3X50=150 marks).
- The amount of material presented in each question will be reduced compared to a typical 50-mark question at this level in previous years.


Foundation Level
Section A: Concepts & Skills (210 Marks)
- Candidates will have a choice of 7 questions from 8, instead of having no choice.
- Each question will be worth 30 marks
- Total will be 7X30=210 marks.
Section B: Contexts & Applications (90 Marks)
- Candidates will choose 2 questions from 3, instead of having no choice.
- Each question will be worth 45 marks
- Total will be 2X45=90 marks.
- The amount of material presented in each question will be reduced compared to a typical 45-mark question at this level in previous years.

These updates can be subjected to new adjustments by gov.ie.
How Important Is Leaving Cert Maths?
Leaving Cert Maths is a requirement for enrollment at almost all Irish universities, and higher Maths gives you a real advantage in maintaining good grades in your college courses.
So if you want to get higher education and want careers in Business, Finance, Engineering, Science, Accounting, Statistics, Medicine, etc., then Leaving Cert Maths will be one the most important subjects for you.
What Are The Highest Points Achievable In Leaving Cert Maths?
If a student gets H1-H6 grades in Maths, they will receive a 25 bonus point. So if you get 100 points (H1) in Maths, your total points will be 125!
Is Leaving Cert Maths Hard?
Leaving Cert Maths is a prerequisite for all higher university degrees. So, yes, naturally, the Leaving Cert Maths is going to be tricky. But how hard will it be for you?
Well, that depends solely on your preparation. It’s a cliche, but preparation is everything! I have seen many students start practicing Maths bit by bit in their 5th year, and it paid off. I personally started doing a few hours of Maths on weekends in my 5th year – and it paid off in the end!
Bonus Tips To Ace Leaving Cert Maths!!
Here are some of my personal tips to ace the Leaving Cert Maths:
1. Practice! Practice! Practice!
Unlike other exams, there is no consistency in what questions and what topics will appear in the exams. Often questions will test you on a few different topics from across the courses.
That is why it can’t be stressed enough how important practice is for Leaving Cert Maths. The more you try, the more you’ll understand and become comfortable with that topic.
There are so many resources available now to help you practice. Starting with the past papers is always the best way forward. Try to find the question patterns and solve those questions regularly as much as you can.
If you need extra help with Leaving Cert Maths, you can join our Online LC Maths Grinds. We provide weekly notes and questions to enhance your Maths skills. Our online classes consist of small groups of 6 kids or less to ensure that every student gets the best guidance possible. We also offer WhatsApp video support for any extra queries outside of our grinds!
You can check our online maths video resources or book a free trial grind to start your journey!
2. Time Management
Time management is also a critical factor in the exam hall. A good starting point is to spend 10 minutes reading the paper to focus on what’s actually asked.
Students often waste valuable time trying hard questions and miss out on the easy ones. It’s okay to move on if you can’t solve the question on the first try. But remember to come back at those unsolved questions as there are marks for attempting all the questions.
3. Attention To Detail
Often, students get nervous or overwhelmed during the exam, which leads them to make silly mistakes. So pay attention to the minor things and take a deep breath if your brain gets foggy.
Read the instructions carefully, figure out what exactly is asked of you. Check all your calculations at least twice. Recheck your formulas and revise as much as you can.
Conclusion
Being one of the mandatory subjects, Maths is an essential subject for acing the Leaving Cert. Many students’ future goals depend entirely on its result.
So give yourself the best chance of fulfilling all your dreams and start your journey to finally break through Maths!
Good luck!
Recommended Reading: Leaving Cert Study Plan
T.J – CEO of Breakthrough Maths
Need help in Maths? Contact the Breakthrough Maths team here.




